Arvestuslik navigatsioon - kõrvalekalded; glissaad
1:60 reegel võimaldab peast, kiiresti lahendada navigatsiooni ülesandeid ja hinnata olukordi, mille puhul navigatsiooni elemendid on omavahel seotud väikeste nurkadega.
Tüüpilised olukorrad
- Kui palju kandub õhusõiduk antud teekonnajoonelt kõrvale 10 NM läbimisel, kui lennatakse 5° kursiveaga.
- Milline on kursiviga või kõrvalekalde nurk, kui õhusõiduki asukoht on 2 km antud teekonnajoonest eemal ja lennatud on 30 km.
- Jätkuks kõrvalekalde nurga leidmisele on vaja leida kursiparandus, jõudmaks tagasi õigele teekonnajoonele või otse sihtkohta.
- Lõpplähenemisel, finaalis õigesse glissaadi sisenemise kõrgus, kindlal kaugusel raja lävest.
Milline peaks olem õhusõiduki kõrgus (QNE raja suhtes) 2 NM kaugusel lävest 3° glissaadi sisenemisel? - Milline on sobiv laskumiskiirus (ROD), valitud lähenemiskiiruse (GS) jaoks, et püsida õigel glissaadil.
Väikeste nurkade puhul, kui nurga suurus α ≤ 15º on sellise nurga sin ja tan väärtused ligikaudu võrdsed nurga suurusega radiaanmõõdus.
sin(α) ≅ α, α rad
tan(α) ≅ α, α rad
Seega võime väikeste nurkade puhul nurga sin ja tan asendada nurga suurusega radiaanides. Mida väiksem on nurga suurus, seda parem on kokkulangevus. Praktikas lennul esinevad kõrvalekalde nurgad on kuni 10º ning enamkasutatavad lõpplähenemise glissaadinurgad on 2º ...5º.
Alljärgnevalt on toodud võrdlusreana mõningate nurkade raadiannmõõdu, nurga sin ja nurga tan väärtused.
α = 5º ehk α = 0,087rad; sinα = 0,087; tanα = 0,087
α = 10º ehk α = 0,175rad; sinα = 0,174; tanα = 0,176
α = 15º ehk α = 0,262rad; sinα = 0,259; tanα = 0,268
Praktilise, kiire arvutuse jaoks tuletame mugavad valemid, arvestades, et harjumuspäraselt mõõdame nurki kraadides.
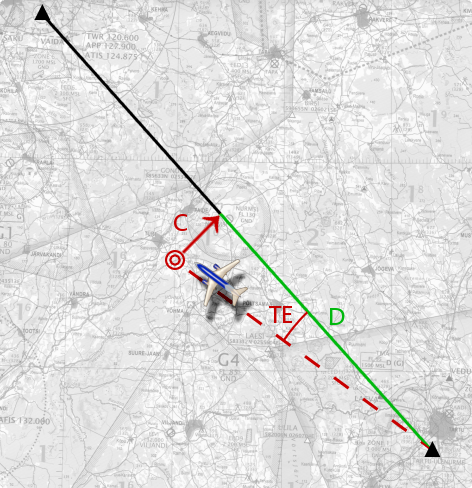
α ≡ TE; D on distants; C on risti kõrvalekalde kaugus.
Olgu väike nurk radiaanides, siis:
| tanα = α = | C |
| D |
1rad = 57,3º ≈ 60º
Modifitseerime valemit kraadide kasutamise jaoks:
| tanα = | αº | = | C |
| 60 | D |
Interaktiivne harjutusülesanne: glissaad



Interaktiivne harjutusülesanne: õigel glissaadil püsimine
Leiame lähenemiskiirusele vastava laskumiskiiruse (ROD). Lähtekohaks on õhusõiduki paiknemine õigel glissaadil, 1 minuti kaugusel raja lävest. Modifitseerime eelnevat valemit:
h = 100 × Z × R
arvestame, et 1 NM = 6080 ft,
h - 1 minutiga kaotatav kõrgus
R - 1 minutiga läbitav distants ehk lähenemiskiirus GS ÷ 60
ROD = 100 × Z × (GS ÷ 60)
ROD on mõõdetud 100ft/min, GS sõlmedes (kts).



Kõrvalekalde skeem